[10000ダウンロード済み√] 立体 の 面積 の 求め 方 335757

／3時 ・角柱や円柱の表面積を求めることができる。 ・角柱や円柱の表面積の求め方を理解する。 本時の学習内容「角柱や円柱の表面積の求め方を考えよう」を知る。 教科書143ページの「考えてみよう」に取り組む。 立体の「表面積」、「底面積面積を求めている間も，音声を消した状態で，動画をループ再生させ，必要なときに確認できるようにする 既習の円の面積の公式，周の長さを公式を黒板に掲示する 4 半径 4 cm，高さが 5 cm の円柱の表面積を求める では，この解き方を参考に他の円柱の底面積（ていめんせき）とは、立体の底面の面積です。 立体は、円柱、円錐、四角柱、三角柱など色々な形状があります。 底面の形状も違うので底面積の求め方も変わります。 例えば、円柱の底面積は、「円の面積」です。 今回は底面積の求め方、計算、円柱、円錐、四角柱、三角柱の底面積について説明します。 底面積と体積の関係、公式は下記が参考になり

三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト

立体 の 面積 の 求め 方

立体 の 面積 の 求め 方-中1 数学 表面積の求め方 表面積の求め方と！円錐の側面積と中心角の簡単な裏ワザをごしょーかい！ページ数少ないです笑 塾で教えてもらいました(((( 学年 中学1年生, 教科書 新編 新しい数学1 東京書籍, 単元 立体の体積と表面積, キーワード 中1,数学,表面積,求め方,まとめ,裏ワザ,簡動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru

円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ

底面積の求め方 図形ごとの底面積の求め方の一覧を下記に示します。 立方体 ⇒ 縦×横 直方体 ⇒ 縦×横 円柱 ⇒ 半径×半径×314 四角柱 ⇒ (上底下底)÷2×高さ 三角柱 ⇒ 底辺×高さ÷2 円錐 ⇒ 半径×半径×314 四角錐 ⇒ (上底下底)÷2×高さ2804そして円柱の体積は「底面積×高さ」で求めることができるので1256×5＝ 628㎤ となります。 まとめ いかがだったでしょうか？立体図形の体積の求め方を理屈から理解できたと思います。A/360 = 1/2 ×

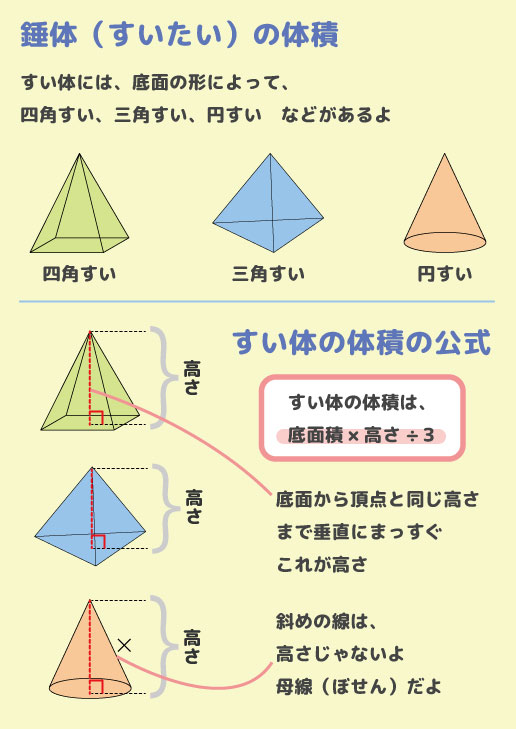
立体の体積 (V)、表面積 (S)または側面積 (F)および重心位置 (G) 「立体の体積 (V)、表面積 (S)または側面積 (F)および重心位置 (G)」からは、以下の計算がご利用いただけます。 立体の体積 (V)、表面積 (S)または側面積 (F)および重心位置 (G) 単位換算 公式計算Tap to unmute If playback doesn't begin shortly, try restarting your device You're signed out Videos you watch may be added to the TV's watch history三角錐や四角錐などの体積は、底面積 $S$、高さ $h$ として、次の式で求められます。 角錐 (かくすい) の体積 \begin{align*} V = \frac{1}{3}Sh \end{align*} 体積 = 底面積 ×

A = 面積 P ＝ 円周(近似式) 円錐 V = 体積 A = 円錐面積 r ＝ d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径立体の体積を求めるには，体積の微分が断面積になることを利用します． すなわち，左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し， x における断面積を S(x) とおきます． 上で復習した面積の求め方と同様にして ⊿V(x)≒S(x)⊿x ≒S(x)立体の表面積の求め方 立体の表面積とは 立体の表面全体の面積のこと をいいます。 立体の表面積の公式も一応示しますが、考え方を理解することができていればわざわざ公式を覚える必要はありません。

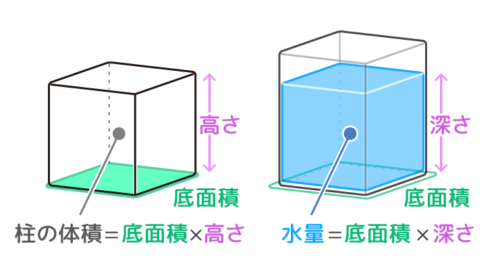
作成中 中学受験 容積 水の問題の解き方は 傾けたり物を沈めたり そうちゃ式 受験算数 2号館 図形 速さ

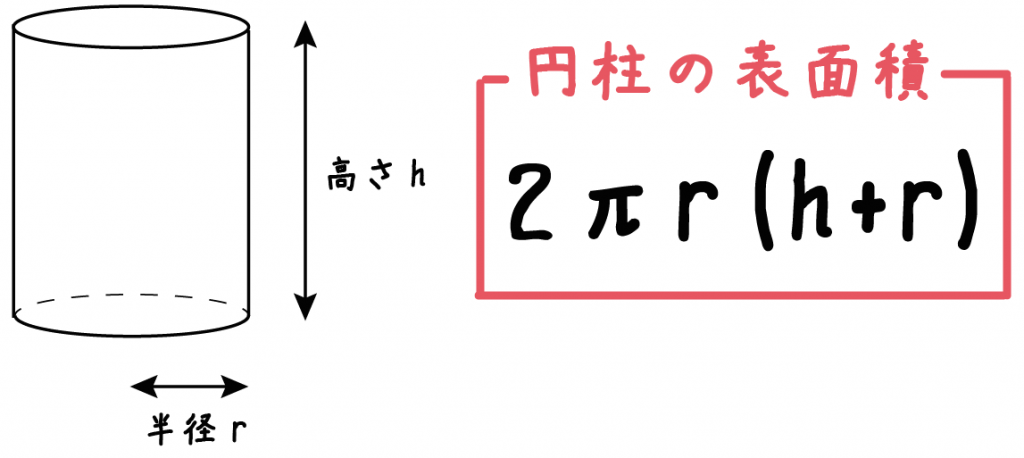
簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

単元 タイトル 解説 画面イメージ 立体の体積 体積ボタン 解説 体積ボタン2 解説 立体（L字型） 解説 6年 分数のかけ算とわり算立体と空間図形 1次の(1)～(4)の立体について下の表を完成させなさい。 3面積（表面積）の求め方について、下の（ ）に当てはまる言葉を入れなさい。 (1) 面積（表面積）の単位は47 7 立体の体積と表面積 133 次の図の直方体の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 137 次の図の立体の体積と表面積を求めよ。 ⑴ ⑵ 135 次の図の円柱の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 134 右 の図は ，円柱とその展開図である。 次の問いに答えよ。

斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル

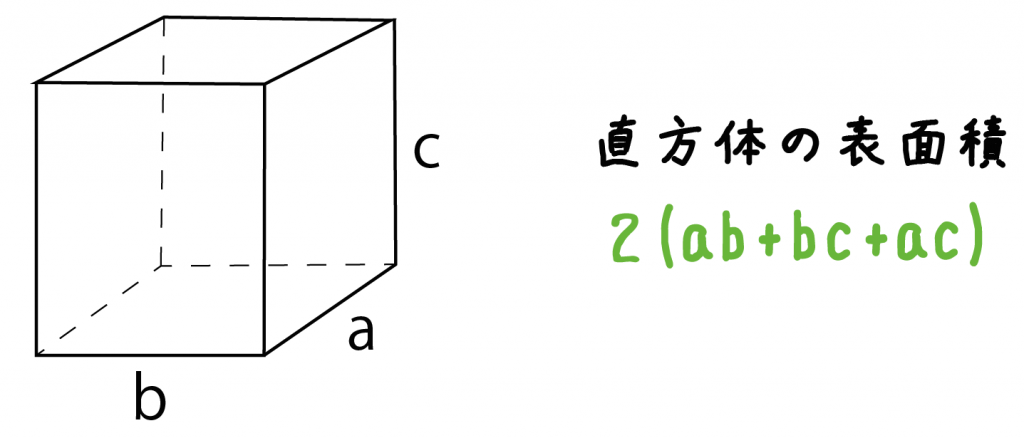
計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

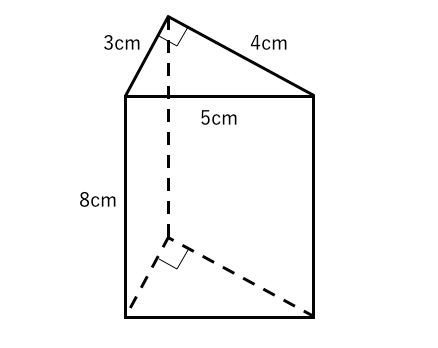
単元名 立体の体積 題材名 「L字型、U字型の立体の体積をくふうして求めよう」 目 標 L字型などの立体の体積の求め方をL字型などの平面の面積の求め方をもとに考え、直方体や立体の 体積の公式を活用して求めることができる。平面上で，円弧を睨む扇形の中心角を，円弧の長さを使って定義しました．このアイデアを全く同様に三次元に拡張したのが 立体角 です．空間上，半径 の球を考え，球の中心を頂点とするような円錐を考えます．この円錐によって切り取られる球面の面積のことを立体角と定義します．次の立体の体積を求めましょう 問題① 底面の形は五角形です 底面を3つの三角形にわけて面積を求めます アの面積 10×3÷2＝15 イの面積 10×5÷2＝25 ウの面積 8×3÷2＝12 合計すると 15＋25＋12＝52 体積は 底面積×高さ だから 52×7＝364 答え 364

うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾

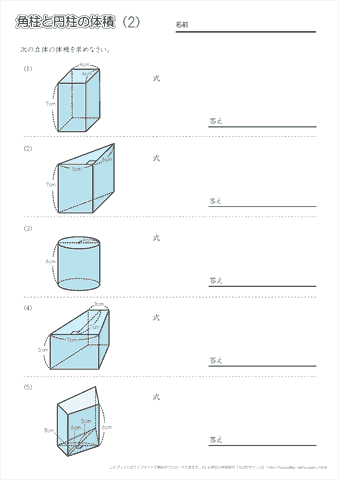
小学６年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生

(1) 展開図のおうぎ形の中心角を求めなさい。 (2) 円すいの側面積を求めなさい。 (3) 円すいの表面積を求めなさい。 基本の考え方 円すいの展開図では、側面がおうぎ形、底面が円となりますので、 「おうぎ形の弧の長さ＝底面の円周」 に着目します。表面積や体積の求め方 (三角柱,四角柱,円柱,球や半球) 表面積や体積の求め方のポイントです。 代表的な三角柱,四角柱,円柱,球や半球などを取り上げて説明しますが、公式ではなく、求めるための手順を覚えるようにしましょう。 問題には公式が使えない立体が多く出てきますので、覚えることを間違えないようにしてください。半径 となっているのですが、 どうして=π ×

空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト

立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun

これで展開図の長方形のよこの長さがわかり、求めたい円柱の側面積がわかりますね。 底面の円周（長方形のよこの長さ）は　2×3×π=6π cm 円柱の側面積は 8×6π=48π cm 2 底面積は　3×3×π=9π cm 2さっそく、例題の表面積を求めてみよう。 底面が2つ、側面が1つだから、 9π×2 60π = 78π になるね！ おめでとう！円柱の表面積の問題を瞬殺できるようになったね！！ まとめ：「円柱の表面積の求め方」は公式なんかいらねえ！体積・表面積 立方体の辺の長さから体積と表面積を計算します。 立方体の体積から辺の長さと表面積を計算します。 直方体の三辺の長さから体積と表面積を計算します。 四面体の6つの辺の長さから体積と表面積を計算します。 正四面体の辺の長さから体積と表面積を計算します。 正四面体の体積から辺の長さと表面積を計算します。 正三角柱の底辺と高さ

中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

ボード 学習 のピン

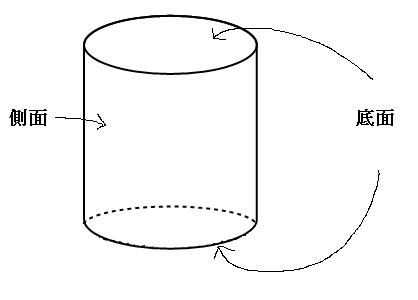
側面積= 側面の面積の総和 だから，円柱，角柱の表面積=底面積×2側面積 となります。 また，「底面積を求めよ」というときは，1つの底面の面積を答えます。立方体の12の辺の長さは等しく、これを $a$ とします。立方体の表面積 $S$ は、次の式で求められます。 立方体の表面積 \begin{align*} V = 6a^2 \end{align*} 表面積 = 一辺 ×漢字のとおり、立体の 「表面の面積」 のことだよ。 底面や側面など、 すべての面の面積 を求めて、たし合わせよう。 立体の表面積を求めるときのポイントは、これだよ。

計算公式 三角柱の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

体積の求め方 計算公式一覧

立体の表面積/扇形 立体の表面積について質問です。 扇形の面積を求め方が 面積=π ×立方体・直方体の体積の求め方｜小学生に教えるための分かりやすい解説 管理人 9月 , 18 / 12月 1, 18 立体の体積という新しい分野なだけに、なかなかイメージしづらかったり、理解しづらい子はこれで平方根の求め方もマスターだ！^^ まとめ：平方根の求め方は√と±つければとりえあずok 平方根の求め方はむちゃくちゃ簡単。 ルートをかぶせて、±を左にくっつける。 最後にルートをはずせるかトライするだけ。 ガンガン平方根を求めていこう！

角柱 円柱の表面積と体積の公式 数学fun

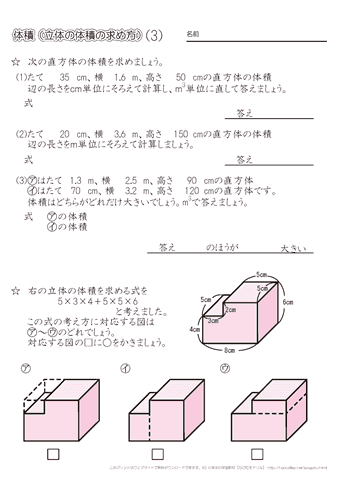
小学５年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生

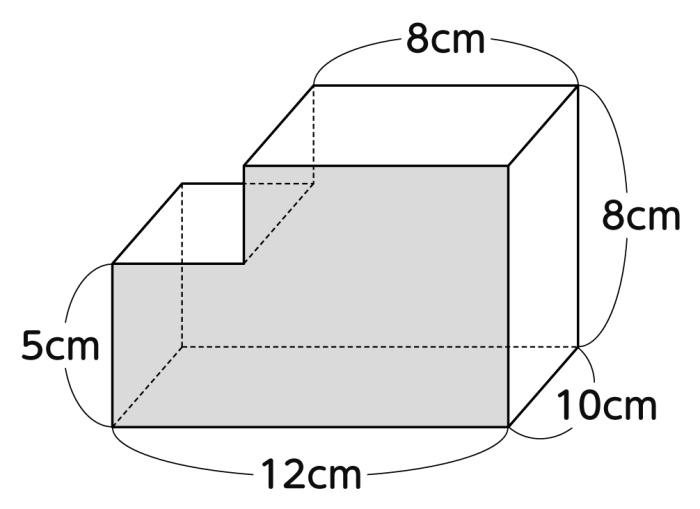
図や立体模型をもとにして、三角柱の体積を求め方を考える。 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 自分の考えを基に、互いに説明し合う。算数への関心・意欲・態度 角柱や円柱の体積の求め方に関心をもち、進んで調べようとする。 数学的な考え方 角柱や円柱の体積の求め方を既習の立体の体積の求め方に帰着して考え， 説明することができる。 数量や図形についての 技能8×4 ＝256（cm³） ②の立方体の体積＝4×4×4＝64（cm³） よって求める立体の体積＝256＋64＝3（cm³）

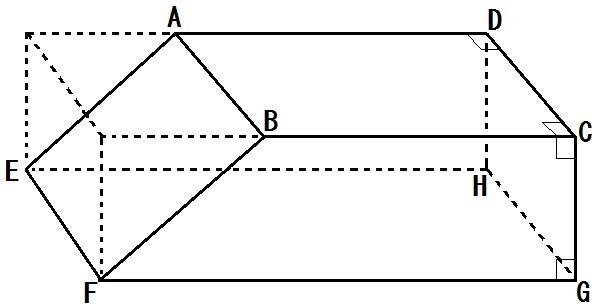
中学数学 空間図形 体積の問題のコツ

中1 中1 数学まとめ 立体の体積や表面積など 中学生 数学のノート Clear

め方の学習を振り返り，本単元の学習を活用できるようにする。第5 学年での直方体や立方体の体積 の求め方を基に，「縦×横」を「底面積」として捉えることにより，四角柱や三角柱，円柱などの体積 も求めることができるということを理解させる。小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題体積・表面積 算数 中学数学 空間図形 立体の 体積の求め方（公式） を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め

角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun

公式を図解 すい体の体積 円すいの表面積の求め方

て先に整理した面積の求め方を参照させる。 （例）底面積s6×4 ＝24 高さh7 自分でノートに見取図をかいて，辺，半径，高さ などに長さを記入する。 見取図の書き方ができるかどうか確認する。 ま と め 今日の学習のまと めをする。 錐体の体積＝立体図形の体積と表面積の練習問題 問題1 次の立体の体積を求めなさい。 → 解答 問題2 次の立体の体積を求めなさい。 ただし、この立体は、どの面も（A）のようになっていて、それぞれの穴は反対の面までつきぬけているものとします。 → 解答

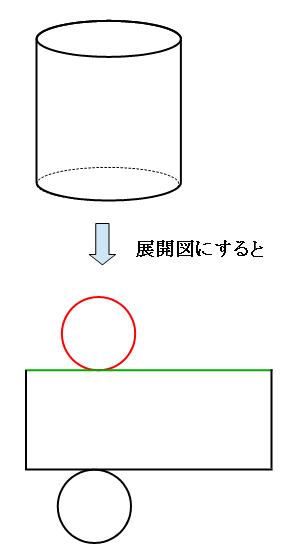
立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか

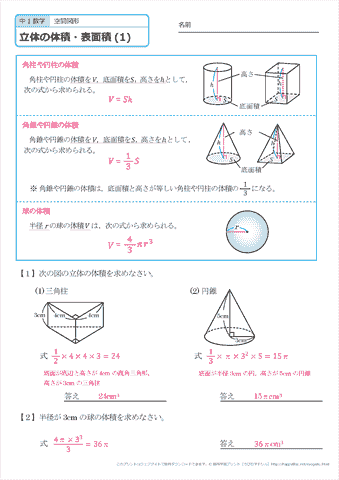
中学１年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

中１数学 すい体の体積と円すいの表面積 数学検定５級 お家でお勉強

体積 複雑な形の立体 算数 教科質問ひろば 進研ゼミ小学講座

体積の求め方 計算公式一覧

公式を図解 すい体の体積 円すいの表面積の求め方

丸棒の重量 円柱の体積と重量の求め方 鉄の場合

立体の表面積を求める 練習問題 苦手な数学を簡単に

円柱の表面積の求め方 立方体 円錐の投影図 中学１年数学 空間図形

中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

ボード 子供の教育 のピン

3分でなるほど 三角錐の体積 表面積の求め方をマスターしよう 数スタ

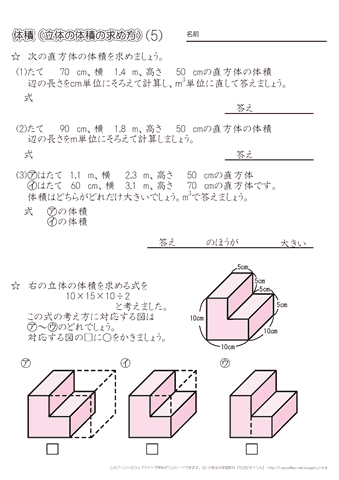
小学５年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生

50 素晴らしい円柱 体積 求め方 リットル 最高のぬりえ

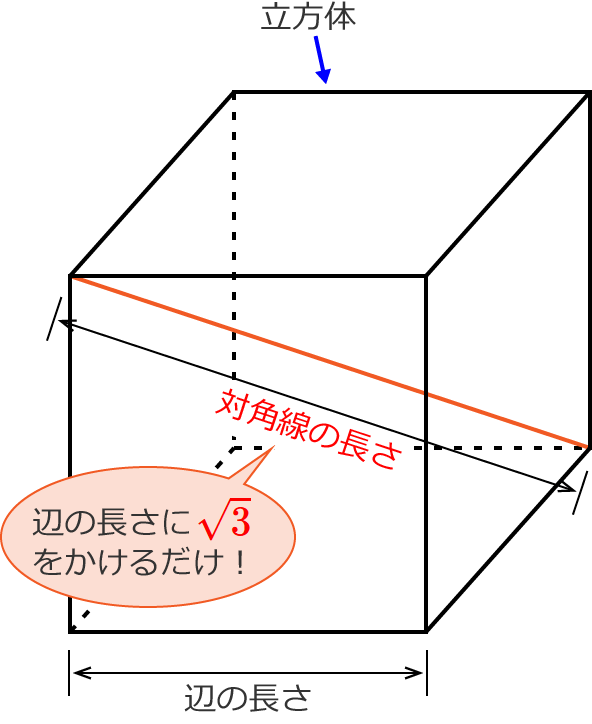
立方体の対角線の長さの求め方

立体の表面積を求める 練習問題 苦手な数学を簡単に

計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

立体図形を斜めに切断した時の体積は 底面積 高さの平均 中学受験 塾なし の勉強法

立体の体積を求める 苦手な数学を簡単に

立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者

円錐の表面積 Youtube

動画で学習 1 角柱と円柱の体積 算数

角錐 円錐の体積と表面積の公式 数学fun

立体 の 表面積 求め 方

0 Abc Ac 1 A Descubre Como Resolverlo En Qanda

円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ

体積について 小学校算数 中学校数学から 身勝手な主張

中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット

中1数学 三角柱 四角柱の表面積の求め方がサクッとわかる 映像授業のtry It トライイット

三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト

地図の体積計測

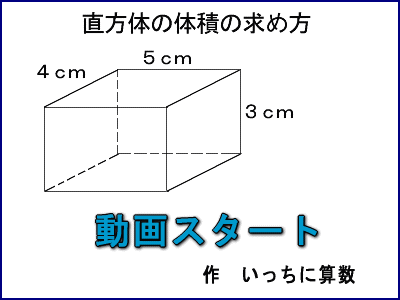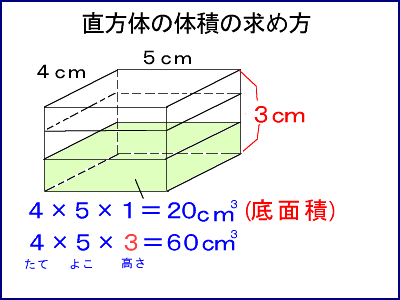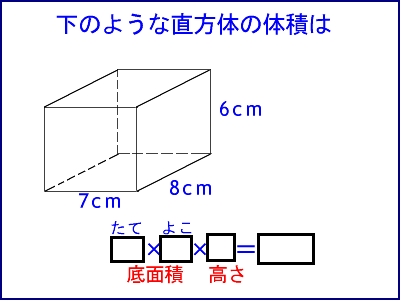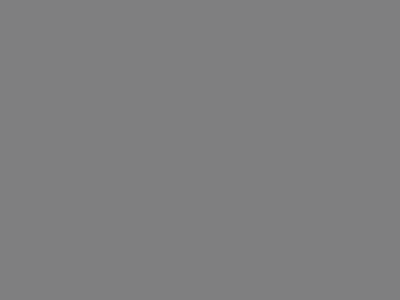
６年算数立体の体積１ 教え方

中1数学 立体の表面積と体積の求め方と練習問題 Pikuu

小学５年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生

立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学

立体の体積と表面積 １ 柱体の表面積

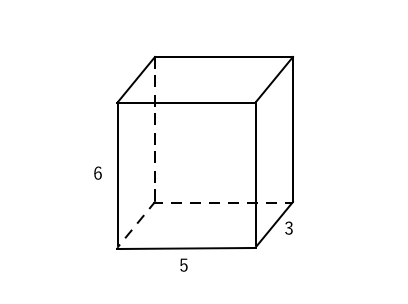
超簡単 体積の求め方 苦手な数学を簡単に

３分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ

面積や体積のかけ算の順序 おかしな算数教育 身勝手な主張

座標を使った体積の問題 円柱が空洞 苦手な数学を簡単に

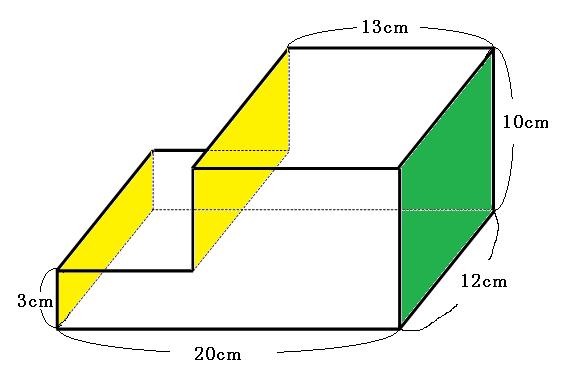
立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか

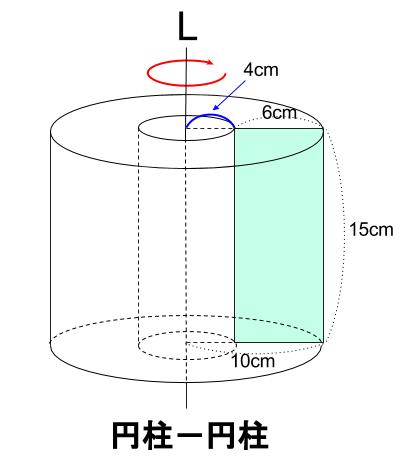
中学数学 回転体 その１ 中学数学の無料オンライン学習サイトchu Su

表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題

Studydoctor立体の体積の求め方と公式 柱体 中学１年数学 Studydoctor

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者

計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

表面積の求め方 計算公式一覧

中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット

斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル

回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学

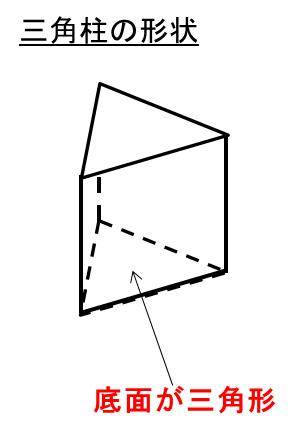
三角柱の表面積 底面積も と体積を求める公式と計算問題 単位との関係 ウルトラフリーダム

体積の求め方 計算公式一覧

６年算数立体の体積１ 教え方

空間図形 円柱の側面積の求め方がわかりません 中学数学 定期テスト対策サイト

Math 積み重ねた立方体の表面積 働きアリ

立体の体積を求める公式

公式を図解 すい体の体積 円すいの表面積の求め方

計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

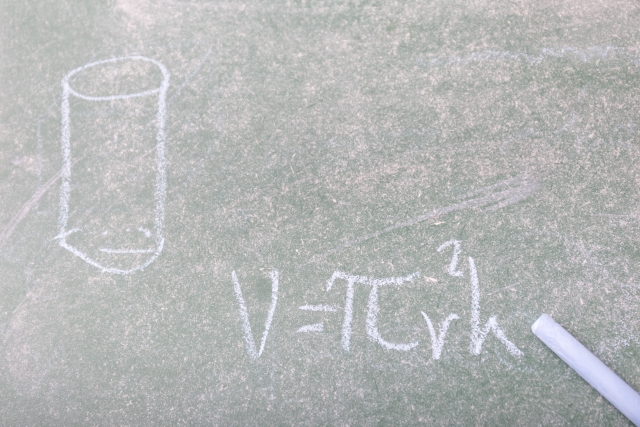
中１数学 円柱の体積 表面積はどうやって求めるの まなビタミン

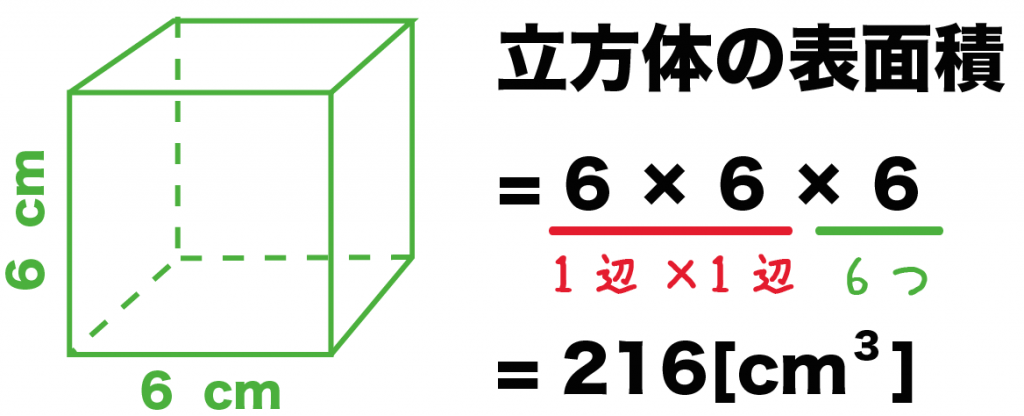
計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

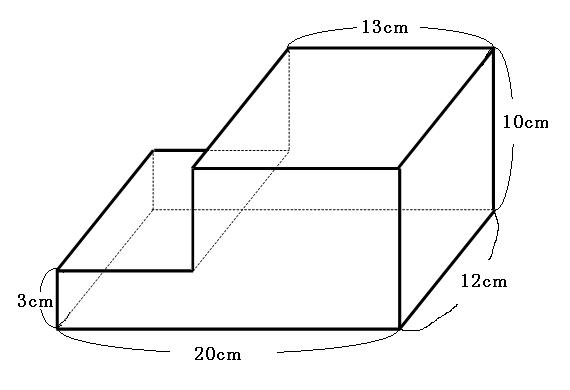
立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか

円錐 側 面積

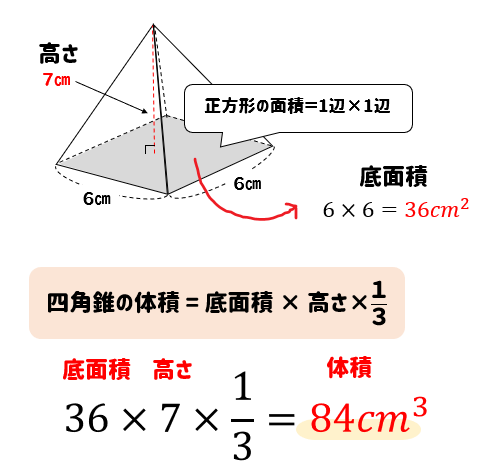
3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ

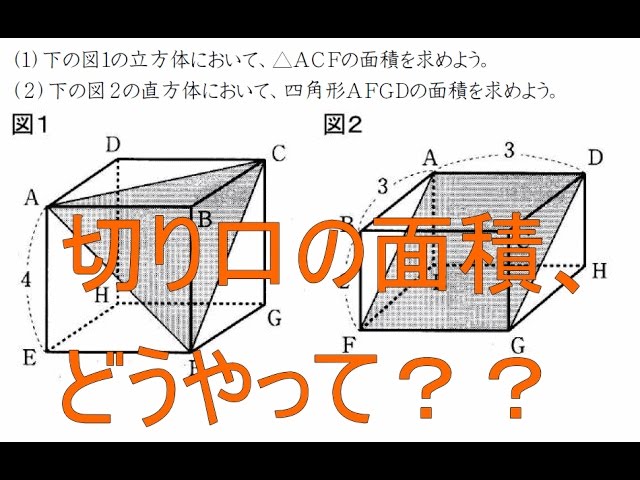
立体の切り口の面積 中学３年数学 Youtube

角柱の体積を求める 5つの方法 Wikihow

角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学

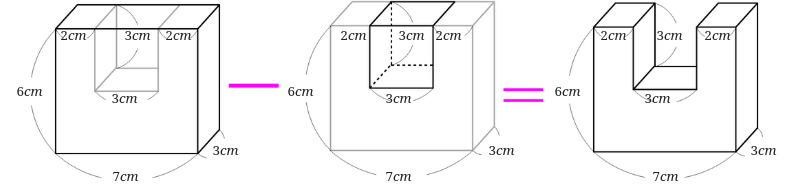
直方体や立方体の体積を求める応用問題の解き方は どうやって教えるといいの みけねこ小学校

3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ

立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム

角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学

ボード 組織 かくしゅう のピン

円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題

体積の求め方 計算公式一覧

至急 この問題を教えてください Clear

面積や体積のかけ算の順序 おかしな算数教育 身勝手な主張

三角柱の体積を求める時にテキストでは2分の1と出ているんですがこれは何なんで Yahoo 知恵袋

台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ

どうして1 3なの 錐の体積の公式の求め方 まなべーと

扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ

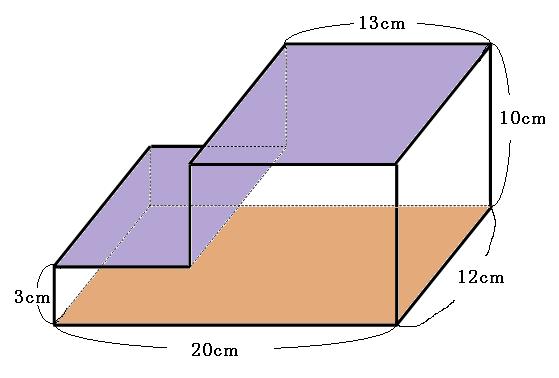
立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか

立体の体積の求め方 何角柱でも何角錐でも同じ